Jenseits von Subroutinen in Abaqus/Standard

Lassen Sie uns untersuchen, wie man neue Keywords verwenden kann, um diesen Prozess in Abaqus/Standard zu rationalisieren.

Sie fragen sich vielleicht: „Welche Art von Problem könnte von der Fähigkeit des Solvers profitieren, einen Step oder gar die gesamte Analyse vorzeitig zu beenden?“

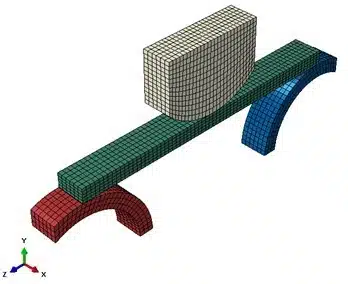
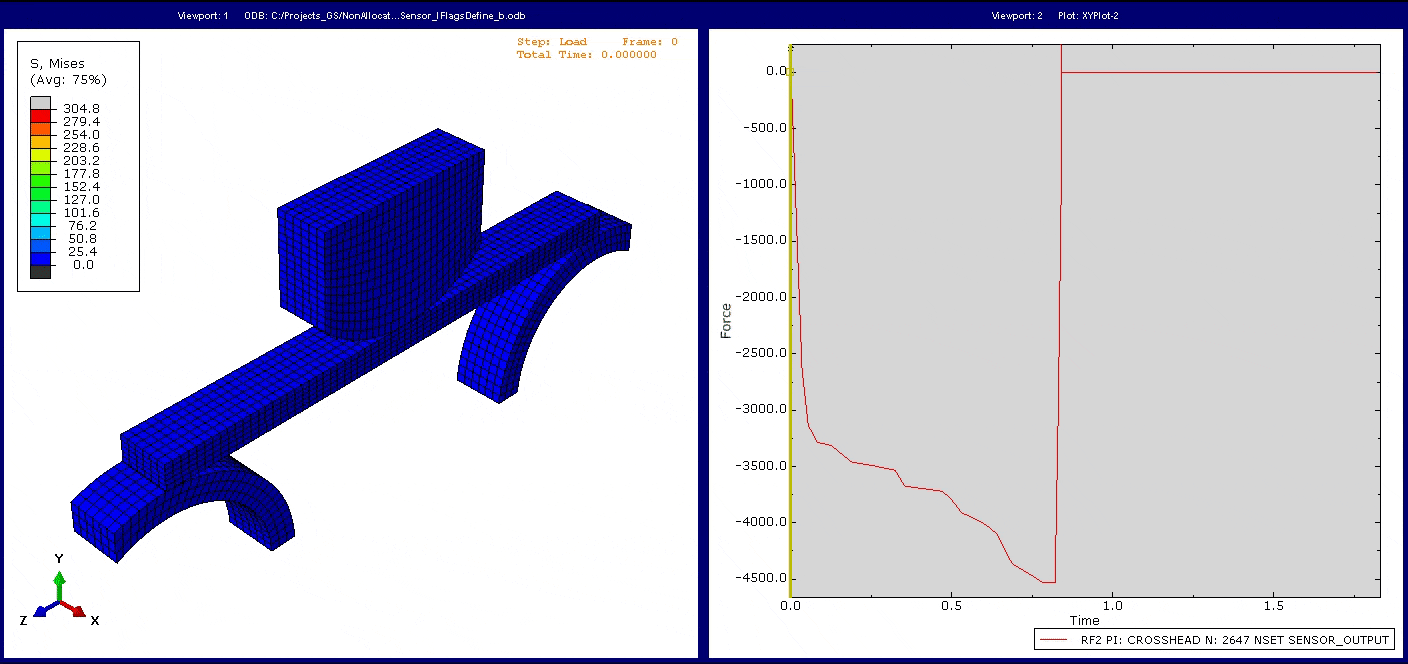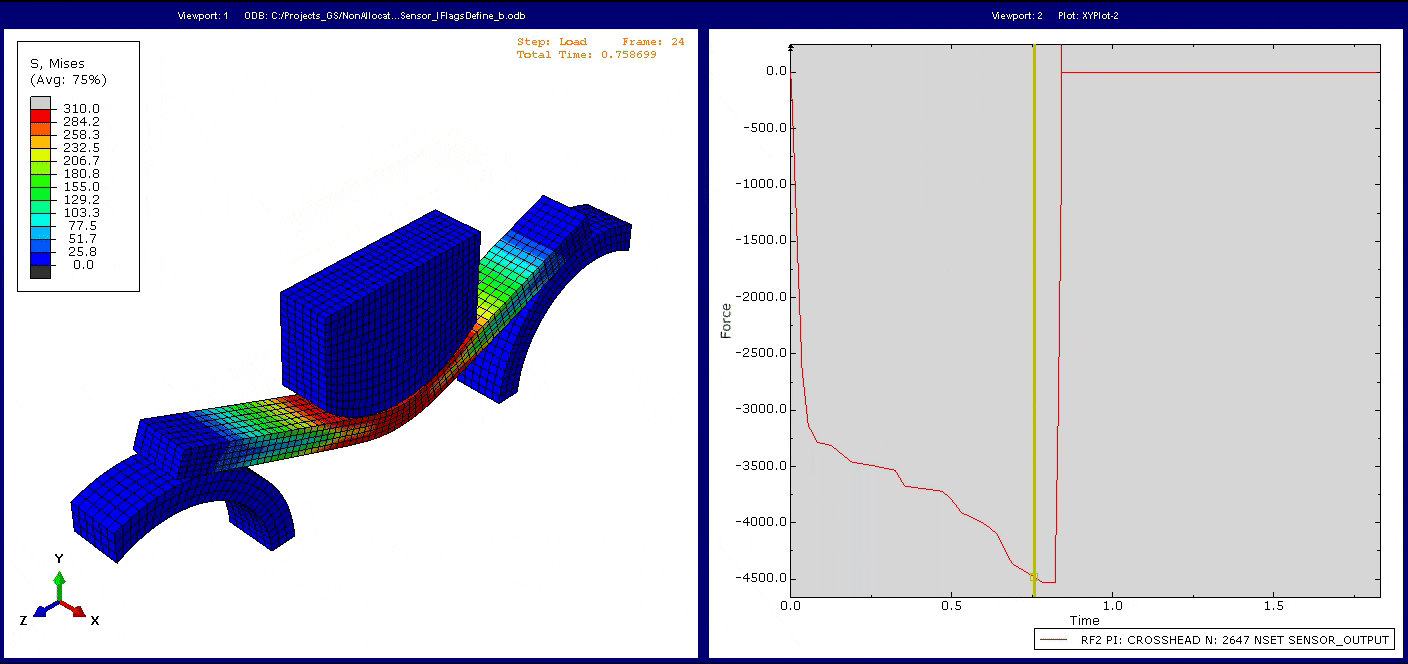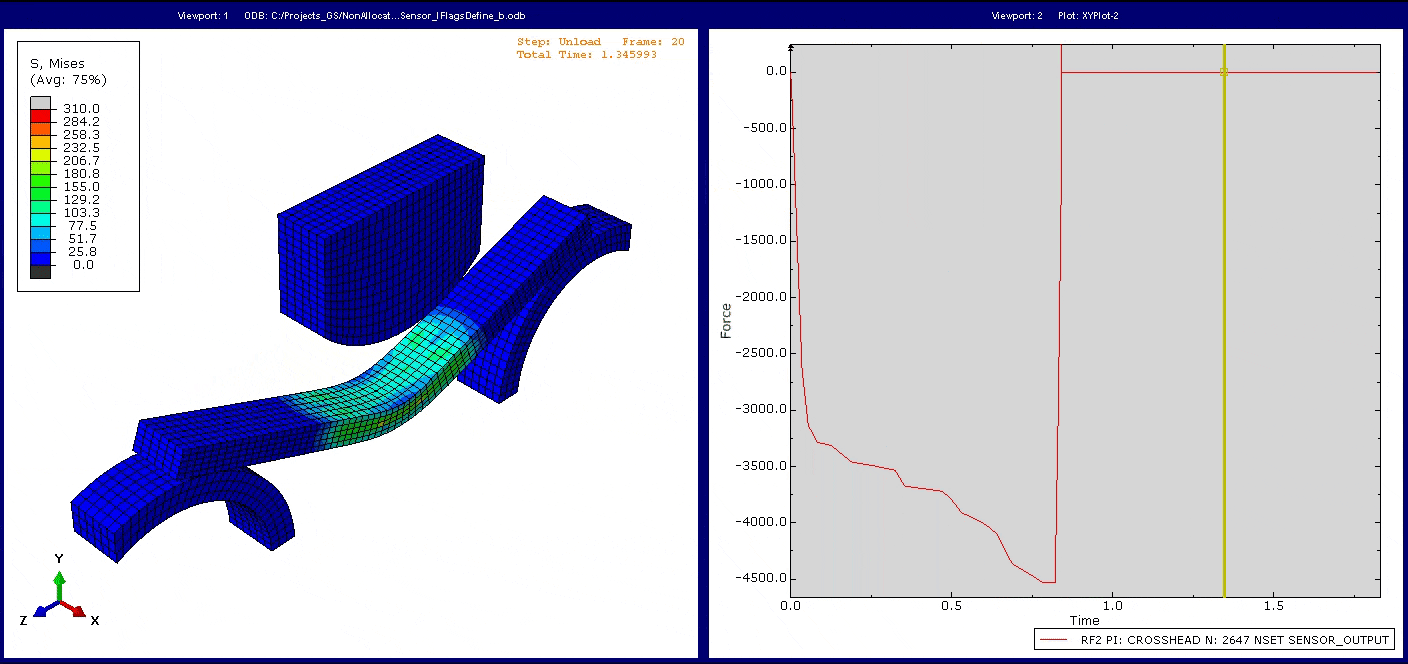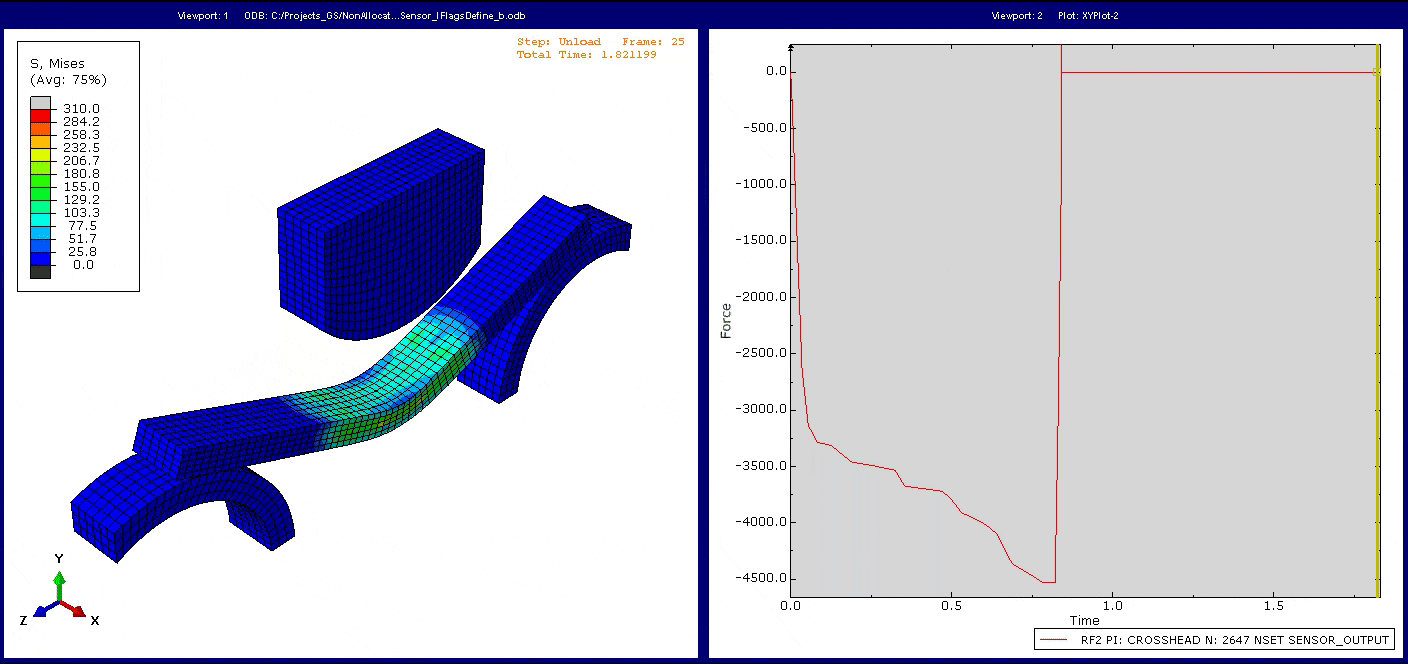
Betrachten wir das folgende Modell als Beispiel. Es handelt sich um eine vereinfachte Darstellung eines 3-Punkt-Biegeversuchs, der während der TECHNIA Simulation Schulungen verwendet wird, um die Auswirkungen verschiedener Nichtlinearitäten auf die Simulationsstrategie zu untersuchen. Alle drei Nichtlinearitäten sind im Modell vorhanden: Kontakt (mit Reibung), geometrische Nichtlinearität und, was für diese Diskussion entscheidend ist, Plastizität, die zu einer bi-linearen elastisch-plastischen Reaktion vereinfacht wird.

Die Simulation umfasst zwei statische Steps. Die beiden unteren Rollen (rot und blau) werden mechanisch fixiert und der obere Stempel (grau) wird nach unten bewegt, um den grünen Balken zu biegen und somit eine plastische Verformung während des ersten Steps hervorzurufen. Im zweiten Step wird der Stempel in seine ursprüngliche Position zurückgebracht, um die elastische Rückfederung und die bleibende Verformung des Balkens zu erhalten.

Um die Konvergenz im Belastungsschritt zu verbessern (bei der die Reaktionskräfte im Balken nur durch die Kontaktkräfte an der Ober- und Unterseite ausgeglichen werden) und vor allem, um den Stempel im Entlastungsschritt effizient in seine Ausgangsposition zurückzubringen wird die Belastung weggesteuert aufgebracht.

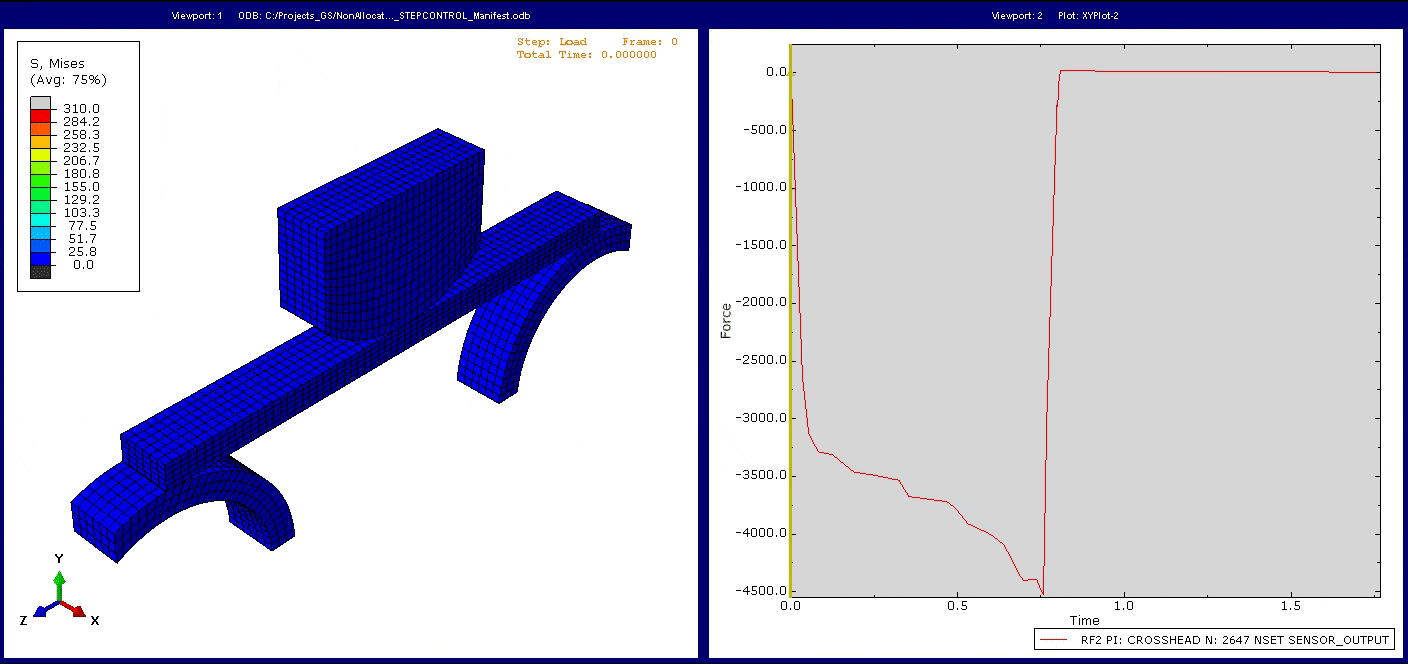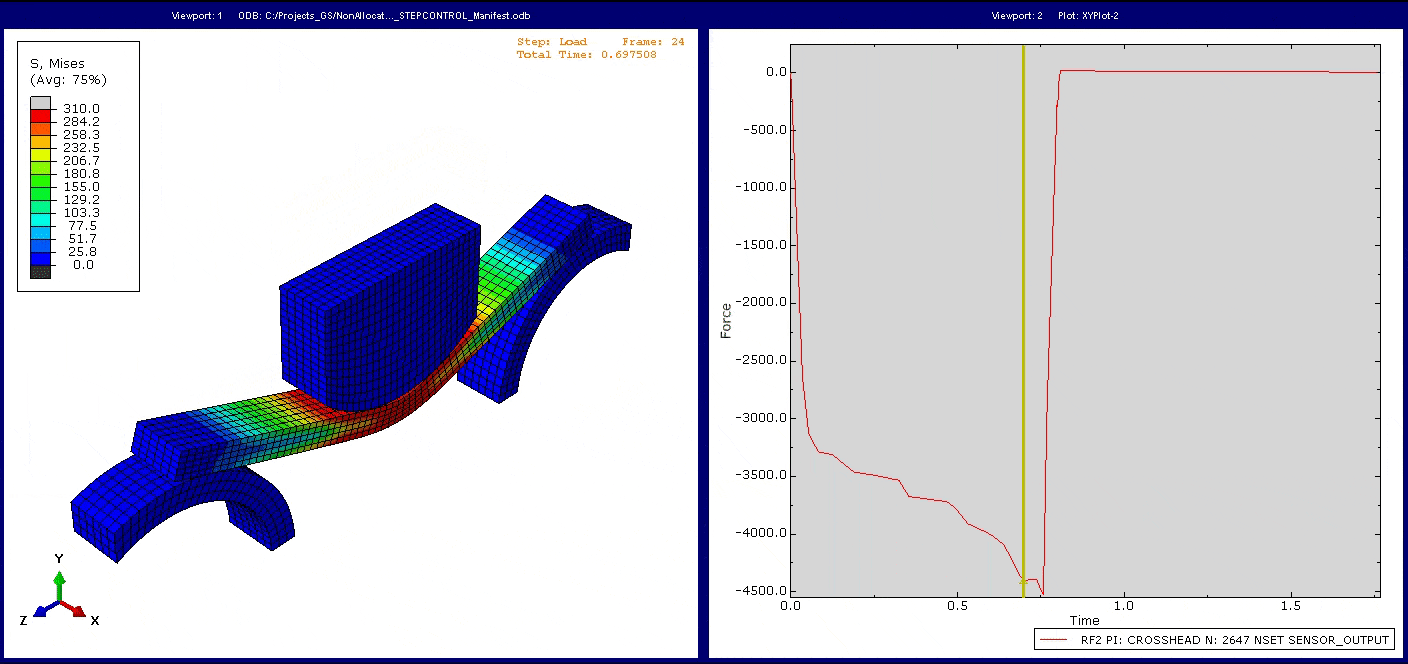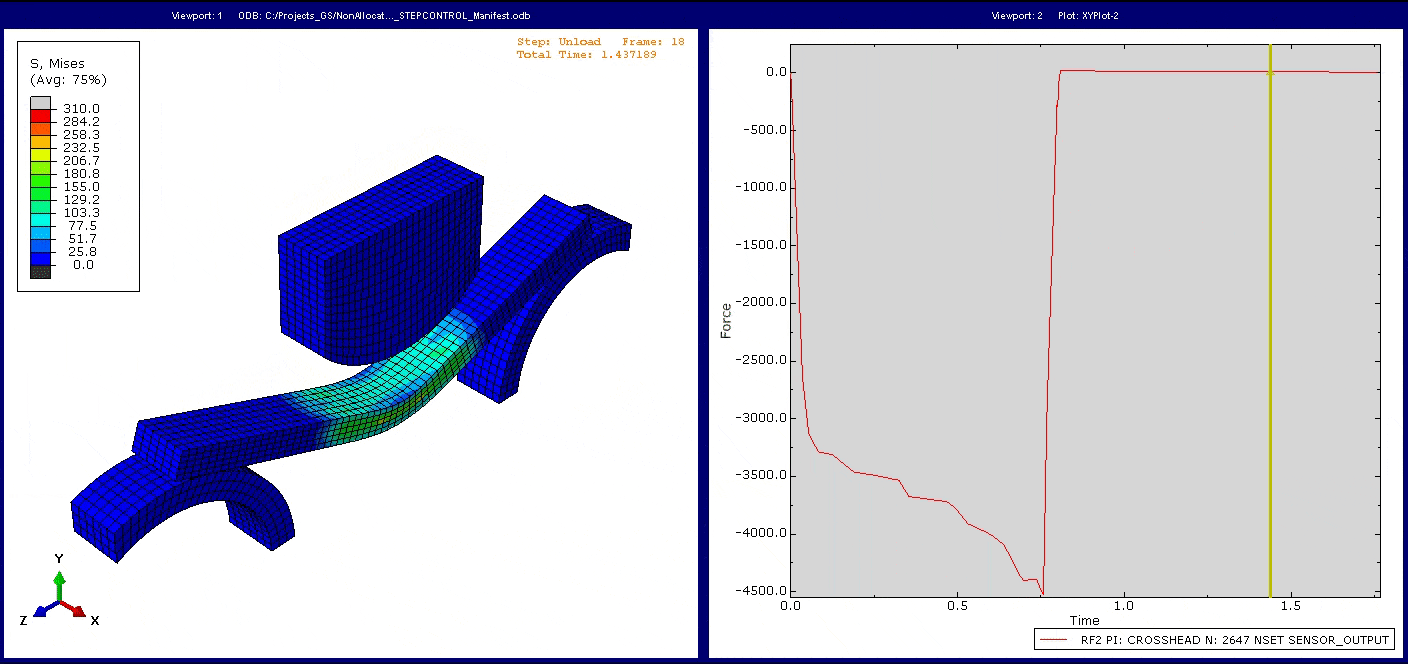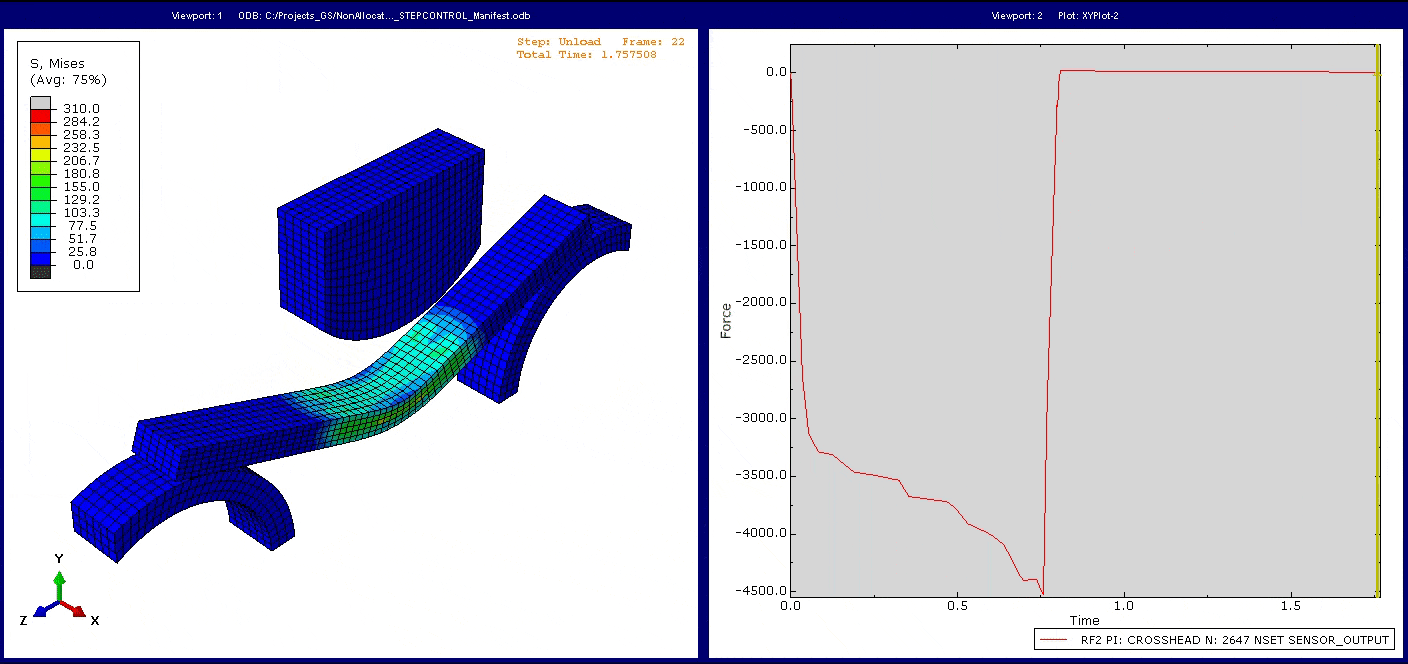
Bei der Simulation dieses Modells beobachten wir die erwartete mechanische Antwort des Systems. Betrachten wir die Reaktionskraft im Stempel über der Zeit, so können wir die Veränderung des Gradienten der Reaktionskraft aufgrund der sich entwickelnden Nichtlinearität im System erkennen.

Hinweis: Wie Sie sehen, geht die Reaktionskraft nicht direkt auf null zurückgeht, wenn der Stempel durch ihre Verschiebung den Kontakt mit dem Balken verliert. In der Simulation wurde im Entlastungsstep eine geringe automatische Stabilisierung eingesetzt, um zu verhindern, dass sich der Balken in x-Richtung bewegt, ohne dass weiteren Kräfte aufgebracht werden. Da die Bewegung des Stempels ebenso mit der Viskosität dieser automatischen Stabilisierung belegt ist, ergibt sich eine geringe Reaktionskraft, die dem entgegenwirkt. Ein Teil der Erkenntnisse aus dem Tutorial besteht darin, zu beurteilen, ob die automatische Stabilisierung das zugrundeliegende mechanische Verhalten signifikant beeinträchtigt.

Das Modell lässt sich in beiden Steps sehr effizient mit einer verschiebungskontrollierten Last lösen, und wir erreichen die gewünschte Reaktion.

Was aber, wenn wir eigentlich eine Reaktionskraft von z. B. -4500N im ersten Schritt erreichen wollen, um den physikalischen Test genauer nachzubilden, statt einfach eine feste Verschiebung anzuwenden und zu sehen, was passiert?

Es gibt mehrere Möglichkeiten, dies zu erreichen, aber je komplexer das Modell und die Studie werden, desto eher kann es sinnvoll sein, die Last weiterhin verschiebungsgesteuert aufzubringen und dem Abaqus-Solver zu erlauben, den Belastungsschritt bei einer vordefinierten Reaktionskraft selbstständig zu beenden.

Welche Möglichkeiten gibt es also in Abaqus/Standard?

Ansatz 1: User Subroutine XIT (Utility)

Die Subroutine XIT erfüllt zwar nicht ganz die von uns angestrebten Ziele, aber es ist ein einfaches Werkzeug, um eine Analyse zu beenden, wenn bestimmte Bedingungen erfüllt sind. Wenn Sie neu in der Anwendung von Abaqus-Subroutinen sind und Hilfe beim Einrichten von Compilern benötigen, lesen Sie unseren Leitfaden oder wenden Sie sich an uns, wenn Sie Hilfe benötigen.

Generell gilt, dass die Verwendung von Abaqus-Subroutinen zwangsläufig einige Fortran-Programmierkenntnisse erfordert. Daher ist dieser Blog keine erschöpfende Anleitung zur Implementierung von Subroutinen, sondern skizziert mögliche Lösungen für dieses spezielle Analyseszenario.

Als Erstes müssen wir das Modell so vorbereiten, dass ein Subroutine damit interagieren kann, indem es z.B. einen Austausch von Daten zwischen dem Solver und dem Subroutine gibt. Für diesen Fall werden wir das Subroutine UAMP verwenden. Einige dieser Änderungen können in Abaqus/CAE durchgeführt werden, aber in diesem Fall werden wir sie von Hand vornehmen. Die notwendigen Keyword Änderungen zu unserem obigen Modell sind unten dargestellt.

In den „Modelldaten“ des Input Files (d.h. vor der Definition des Steps) müssen wir eine Amplitude definieren, die die Subroutine UAMP aufruft, und zudem ein Knotenset an der Stelle, an der wir einen „Sensor“ zur Überwachung der Reaktionskraft definieren wollen. In diesem Fall ist das der Knoten auf dem Stempel, an dem die Verschiebung aufgebracht wird.

In der der Definition des Steps definieren wir zudem eine Dummy CLOAD mit einer Kraft von Null und der zuvor definierten Amplitude. Die Verschiebung auf den Stempel wird weiterhin mit der Standard-RAMP-Definition aufgebracht.

Und schließlich fordern wir im Step einen History Output für die Reaktionskraft am Sensor an, die wir an die Subroutine für die bedingte Prüfung übergeben.

Nun haben wir also das Abaqus Input File so angepasst, dass nützliche Daten an ein Subroutine übergeben werden. Wir müssen nun die Subroutine erstellen, und verwenden hierzu die UAMP-Vorlage aus der Dokumentation als Grundlage. Wir müssen nur noch die folgenden Anweisungen hinzufügen, die Folgendes bewirken:

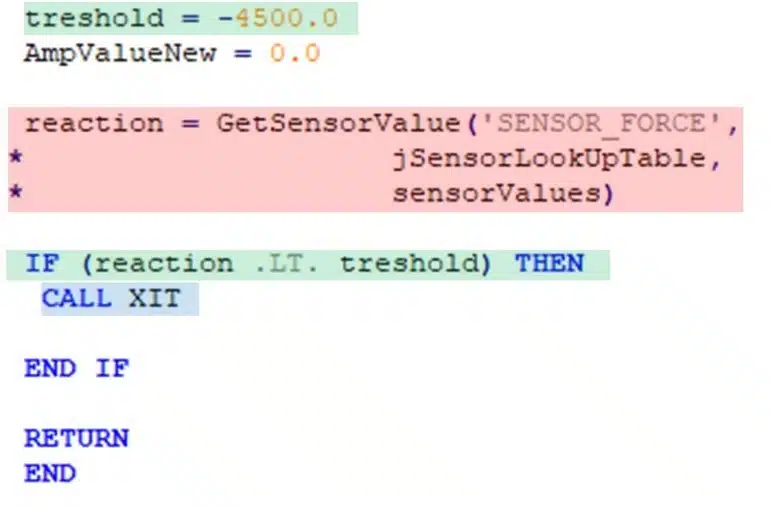
• Extrahieren der Sensordaten aus dem Solver nach jedem abgeschlossenen Lösungsinkrement (roter Kasten)
• Überprüfung der Reaktionskraft, um festzustellen, ob diese kleiner als der vorgegebene Zielwert ist (grüner Kasten)
• Beenden der Simulation, wenn die Überprüfung positiv ausfällt (blaues Feld)

Der XIT-Befehl wird von den meisten Abaqus-Subroutinen erkannt; wir haben hier nur UAMP verwendet, um später andere Optionen zu untersuchen.

Unter der Voraussetzung, dass ein Fortran-Compiler installiert und mit der ausgeführten Version von Abaqus verknüpft ist, können wir diesen Job mit den folgenden Kommandozeilenoptionen ausführen:

abaqus job=<Job-name> user=<subroutine_name>.f

Wenn wir den Job ausführen, läuft die Lösung wie gewohnt ab, bis wir das erste konvergierte Inkrement erreichen, bei dem die Reaktionskraft am Sensorknoten größer ist als der vom Benutzer festgelegte Schwellenwert. An diesem Punkt wird der XIT-Befehl ausgeführt, und die Analyse wird ordnungsgemäß beendet.

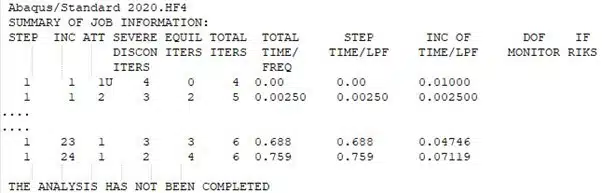
In der Statusdatei wird die Meldung „THE ANALYSIS HAS NOT BEEN COMPLETED“ ausgegeben, da der Solver feststellt, dass etwas passiert ist, das ihn daran hindert, das Ende des Ladevorgangs zu erreichen.

Das ist zwar recht übersichtlich und einfach einzurichten, entspricht aber in zweierlei Hinsicht nicht unseren Anforderungen:

• Die Analyse wird an dem Punkt beendet, an dem die Reaktionskraft den gewünschten Schwellenwert erreicht. Eigentlich wollten wir aber, dass der Step beendet wird und die Analyse mit dem Entlastungsstep fortgesetzt wird
• Die Kontrolle des Abbruchpunkts ist nicht sehr präzise, insbesondere wenn wir die Auswahl der Inkremente automatisiert Abaqus überlassen. So beträgt bei Inkrement 23 berechnete Reaktionskraft -4473 N (knapp unter der Abbruchschwelle) und bei Inkrement 24 schon -4598 N, also 98N über der Abbruchschwelle, wenn der XIT-Befehl ausgeführt wird

Ansatz 2: UAMP-Subroutine Utility lFlagsDefine(iConcludeStep)

Als Verbesserung unseres ersten Ansatzes mit Verwendung der XIT-Funktion bietet das UAMP-Subroutine eine integrierte Variable, die dem Solver mitteilt, ob ein Schritt fortgesetzt oder beendet werden soll. Durch Anpassung der Subroutine und des Input Files können wir einen Schritt bei einer bestimmten Reaktionskraft beenden und nahtlos zum nächsten Schritt übergehen. Diese Methode bringt uns unserem Ziel schon näher, wobei das Erreichen des genauen Schwellenwerts weiterhin eine Herausforderung bleibt.

Als Erstes stellen wir fest, dass es eine praktische eingebaute Variable in der UAMP-Subroutine gibt, die wir setzen können, um dem Solver eine Information mitzuteilen.

Beim Setzen von:

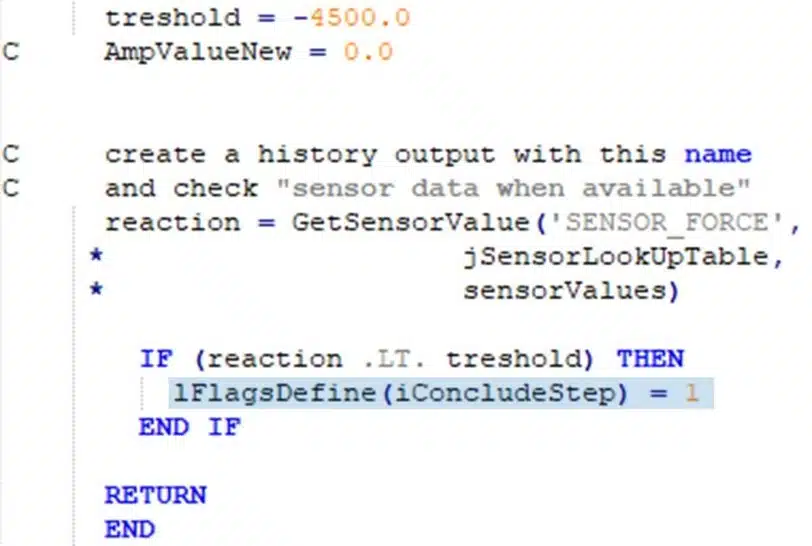
• lFlagsDefine(iConcludeStep) = 0 … sollte der Schritt zum nächsten Inkrement fortgesetzt werden
• lFlagsDefine(iConcludeStep) = 1 … soll der Schritt bei diesem Schritt enden

Indem wir also einfach den XIT-Befehl durch lFlagsDefine(iConcludeStep) = 1 in unserem Subroutine ersetzen, erreichen wir das gleiche Ergebnis mit einer Funktionalität, die bereits in das Subroutine eingebaut ist, und nicht mit einem externen Befehl. Dies stellt eine Verbesserung der Funktionalität im Vergleich zu XIT dar, da nur der Step beendet wird und der Solver mit dem nachfolgenden Step der Entladung fortfährt.

Im zweiten/Entlastungsschritt geht der Solver einfach zum nächsten Step über, da der erste Step beendet wurde. Allerdings ergibt sich dadurch ein neues (kleines) Problem, da der Sprung von einer großen Verschiebung des Stempels am Endpunkt des Beladungsschritts zu einer Nullverschiebung im Entlastungsschritt zu groß.

Dies erfordert ein paar weitere Änderungen in unserem Input File zur Steuerung der Verschiebung des Entlastungsstep über eine AMPLITUDE, die wir ebenfalls in der Subroutine UAMP berechnen. Durch die Verfolgung der Step-Zeit, der Gesamtzeit und der Verschiebung des Stempels können wir einen Prozess erreichen, der:

• den Belastungsschritt bis zu einem benutzerdefinierten Schwellenwert der Reaktionskraft durchläuft
• den Belastungsschritt an dem Punkt beendet, an dem die bedingte Anweisung erfüllt ist
• den Entlastungsschritt fortsetzt und den Endpunkt des ersten Schritts als Startpunkt für den zweiten Schritt verwendet

Wenn wir uns die Ergebnisse anschauen, sehen wir, dass wir alle unsere Anforderungen erfüllen. Allerdings gibt es einen Weg, wie wir dieses Ergebnis deutlich einfacher erreichen und zudem mit höherer Genauigkeit.

Ansatz 3: *STEP CONTROL Keyword

Das Keyword „step control“, das mit dem letzten Abaqus-Update eingeführt wurde, löst auf elegante Weise unser Problem der Schrittbeendigung. Mit nur ein paar Zeilen im Input File können wir Bedingungen für die Beendigung eines Steps definieren und das Step Inkrement verfeinern, wenn wir uns dem Abbruchpunkt nähern. Diese systemeigene Funktionalität vereinfacht unseren Arbeitsablauf erheblich und macht Abaqus-Subroutinen und Compiler für unser Problem überflüssig.

Um die Step Steuerung in unserem Arbeitsablauf zu verwenden, müssen wir lediglich unser ursprüngliches Abaqus-Modell des Be- und Entlastungsszenarios ändern:

• Definieren Sie hierzu einen Reaktionskraftsensor für den Steuerknoten des Stempels direkt in Abaqus/CAE oder mithilfe von Keywords, genauso wie wir es vor der XIT-Subroutine getan haben
• Fügen Sie die folgenden Keywords und Optionen in den Verlaufsdaten für den Ladevorgang in die Eingabedatei ein, wie unten gezeigt:

Diese beiden Zeilen in der Eingabedatei definieren die folgende Abfolge von Ereignissen:

• Erstellen Sie eine STEP CONTROL-Definition mit dem Namen STEP_SENSOR, um einige bedingte Kontrollen für diesen Step zu konfigurieren (mehrere Kontrollen pro Step sind möglich)
• Beenden Sie den Step, wenn die bedingte Anweisung erfüllt ist, und verwenden Sie die automatische Step-Time Verfeinerung, wenn sich die Lösung der Abbruchbedingung nähert.
• Die bedingte Anweisung, die das Ende des Steps wie zuvor auslöst lautet: wenn die Reaktionskraft am Steuerknoten des Stempels, den wir zuvor definiert haben (SENSOR_FORCE), einen Wert von -4500 N unterschreitet
• Wenn die Sensorkraft einen Wert von -4300 N unterschreitet, wird von der automatischen Step-Time Steuerung, die durch das Keyword STATIC definiert ist, auf ein feineres Zeitinkrement gewechselt.

Da wir nun keine Subroutine und keinen Fortran Compiler benötigen, können wir den Job einfach mithilfe des gewohnten Kommandos starten:

abaqus job=<Job-name>

Allerdings laufen wir in ein ähnliches Problem wie zuvor, dass der Sprung in der Belastung zu groß ist, sodass der Entlastungsstep schon im ersten Inkrement nicht konvergiert. Glücklicherweise gibt es auch hierfür ein neues Keyword. Dieses verwendet die Restart Funktionalität von Abaqus und erweitert bzw. vereinfacht diese deutlich:

• Erstellen Sie ein Input File mit allen Modelldaten sowie nur dem Belastungsstep und der zuvor beschriebenen STEP CONTROL Zeile (*ACTION = END STEP beendet den Step. *ACTION = END zum Beenden der gesamten Analyse ist ebenso verfügbar).
• Erstellen Sie ein separates Input File, welches nur die Informationen zum Entlastungsstep enthält, siehe unten)

• Erstellen Sie ein zusätzliches Input File, welches das *MANIFEST Keyword enthält und auf die zuvor definierten Input Files referenziert

Führen Sie den Manifest Job so aus wie jedes andere Input File. Die beiden referenzierten Input Files werden dann nacheinander ausgeführt. Die BASE STATE = YES Option stellt sicher, dass der zweite Step das Ende der ersten Simulation als Ausgangspunkt verwendet.

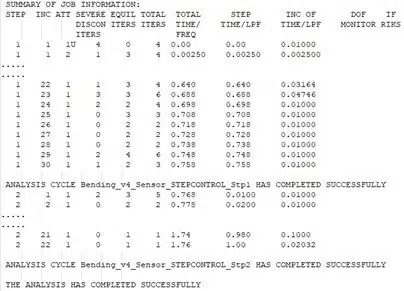
Ein zusätzlicher Benefit ist, dass die Ergebnisse alle in einer einzigen Abaqus Dateistruktur inklusive nur einer odb Datei enthalten sind. Das Status File sieht wie folgt aus.

Das heißt wir können alle Ergebnisse aus der odb Datei der Manifest Analyse gewinnen, die Daten beider Steps sind verfügbar. Dies wäre bei einer Restart Analyse nicht der Fall gewesen und wir hätten zusätzliche Tools verwenden müssen, um die Ergebnisse zu einer odb Datei zu kombinieren.

Brauchen wir noch Subroutinen in Abaqus?

Der Abaqus-Solver wird ständig verbessert und bietet allen Anwendern über das Input File erweiterte Möglichkeiten.

Jetzt ist es ganz einfach, Ihrer Abaqus/Standard-Analyse einen Hauch von Autonomie hinzuzufügen, selbst wenn Sie sich gerade erst mit den Grundlagen der Input File Struktur vertraut gemacht haben. Und obwohl Abaqus-Subroutinen wertvolle Werkzeuge für viele komplexe Aufgaben sind, treten sie in diesem speziellen Prozess in den Hintergrund.

Wenn Sie neue Funktionalitäten in Abaqus kennenlernen möchten, dann wenden Sie sich an die Experten von TECHNIA Simulation und informieren Sie sich über das Continuous Learning Program für Abaqus.